本文目录
利用五巧板,你还能通过怎样的拼图验证勾股定理
答案： 解析： 拼图如图： 验证：∵以c为边的正方形的面积正好是一副五巧板的面积即①＋②＋③＋④＋⑤的和． 而以a为边长的小正方形面积是①＋③之和， 以b为边长的小正方形面积是②＋④＋⑤之和． 即以a、b为边的正方形面积之和正好是一副五巧板的面积（①＋②＋③＋④＋⑤） ∴就有a2＋b2＝c2． 提示： 拼图如图： 验证：∵以c为边的正方形的面积正好是一副五巧板的面积即①＋②＋③＋④＋⑤的和． 而以a为边长的小正方形面积是①＋③之和， 以b为边长的小正方形面积是②＋④＋⑤之和． 即以a、b为边的正方形面积之和正好是一副五巧板的面积（①＋②＋③＋④＋⑤） ∴就有a2＋b2＝c2．
七巧板还有哪些变身,四,五巧板
有智力七巧板、双圆七巧板、日本七巧板、变形七巧板、九巧板、五巧板、四巧板、益智图这些变化。
尽管七巧板可以做出很多不同的图形，但是形状上就有一个很大的限制：不能做出带有曲线的图形。另外，七巧板始终有些图形不能做出。于是，古今中外就设计出与七巧板类似的游戏。
七巧板又称七巧图、智慧板，是中国民间流传的智力玩具。它是由宋代的宴几演变而来的，原为文人的一种室内游戏，后在民间演变为拼图板玩具。
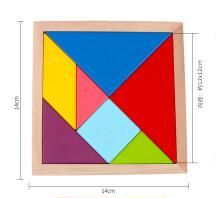
利用五巧板,你还能通过怎样的拼图验证勾股定理
首先介绍勾股定理的两个最为精彩的证明，据说分别来源于中国和希腊。
1．中国方法：画两个边长为(a+b)的正方形，如图，其中a、b为直角边，c为斜边。这两个正方形全等，故面积相等。
左图与右图各有四个与原直角三角形全等的三角形，左右四个三角形面积之和必相等。从左右两图中都把四个三角形去掉，图形剩下部分的面积必相等。左图剩下两个正方形，分别以a、b为边。右图剩下以c为边的正方形。于是
a^2+b^2=c^2。
这就是我们几何教科书中所介绍的方法。既直观又简单，任何人都看得懂。
2．希腊方法：直接在直角三角形三边上画正方形，如图。
容易看出，
△ABA’ ≌△AA'C 。
过C向A’’B’’引垂线，交AB于C’，交A’’B’’于C’’。
△ABA’与正方形ACDA’同底等高,前者面积为后者面积的一半，△AA’’C与矩形AA’’C’’C’同底等高，前者的面积也是后者的一半。由△ABA’≌△AA’’C，知正方形ACDA’的面积等于矩形AA’’C’’C’的面积。同理可得正方形BB’EC的面积等于矩形B’’BC’C’’的面积。
于是， S正方形AA’’B’’B=S正方形ACDA’+S正方形BB’EC，
即 a2+b2=c2。
至于三角形面积是同底等高的矩形面积之半，则可用割补法得到（请读者自己证明）。这里只用到简单的面积关系，不涉及三角形和矩形的面积公式。
这就是希腊古代数学家欧几里得在其《几何原本》中的证法。
以上两个证明方法之所以精彩，是它们所用到的定理少，都只用到面积的两个基本观念：
⑴ 全等形的面积相等；
⑵ 一个图形分割成几部分，各部分面积之和等于原图形的面积。
这是完全可以接受的朴素观念，任何人都能理解。
我国历代数学家关于勾股定理的论证方法有多种，为勾股定理作的图注也不少，其中较早的是赵爽（即赵君卿）在他附于《周髀算经》之中的论文《勾股圆方图注》中的证明。采用的是割补法：
如图，将图中的四个直角三角形涂上朱色，把中间小正方形涂上黄色，叫做中黄实，以弦为边的正方形称为弦实，然后经过拼补搭配，“令出入相补，各从其类”，他肯定了勾股弦三者的关系是符合勾股定理的。即“勾股各自乘，并之为弦实，开方除之，即弦也”。
赵爽对勾股定理的证明，显示了我国数学家高超的证题思想，较为简明、直观。
西方也有很多学者研究了勾股定理，给出了很多证明方法，其中有文字记载的最早的证明是毕达哥拉斯给出的。据说当他证明了勾股定理以后，欣喜若狂，杀牛百头，以示庆贺。故西方亦称勾股定理为“百牛定理”。遗憾的是，毕达哥拉斯的证明方法早已失传，我们无从知道他的证法。
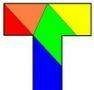
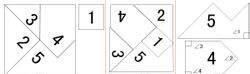
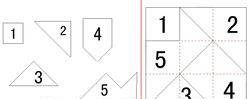
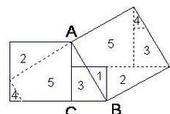上面 最后那个图就是证明勾股定理的拼法。
希望能帮到您。
五巧板怎么做雪糕形状
***.cn/Dispbbs.asp?boardid=10&ID=1783
这里有介绍~
以上就是关于五巧板拼图大全 ,利用五巧板,你还能通过怎样的拼图验证勾股定理的全部内容，以及五巧板拼图大全 的相关内容,希望能够帮到您。
